Three Ways to Get Nerds in an Argument
Best Ways to Get Nerds in an Argument
People don’t think that nerds are usually the fighting type. However, there are some things that nerds get very angry about other nerds about. These are three of those ways that I have been thinking about.
1) Bigger Processor Caches vs. Smaller, Smarter Processor Caches

This is the big difference between Intel and AMD processors. Processor caches are tiny bits of incredibly fast RAM that is located inside of the processor. Most processors have three caches. There is an incredibly fast, small cache (often called L1). There is also a medium-speed, medium-sized cache (called L2). Also, there is a third larger, slower cache called L3. These caches are made out of SRAM, which is just faster RAM.
Now that we have gone over the basics of this confusion, here is where the argument starts. AMD believes that the caches should be more massive. So, if you purchase an AMD processor, you will wind up with a larger cache than an Intel processor. However, Intel believes that the caches should be smaller yet smarter. This debate between hardware experts is possibly one of the most significant discussions in Computer Science.
2) Placement of Curly Brackets
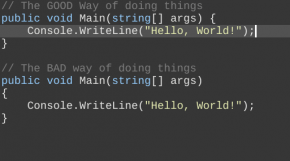
As you can see here, there is a significant dispute between software programmers about where curly brackets go. In most languages, there are curly brackets that go after if statements, functions, and other similar statements to specify the code lines which are affected by that statement.
However, some people want to put the first curly bracket on a different line than the statement, which drives most programmers and me that like doing things the right way where the curly bracket goes directly after the statement and before the line changes. It’s incredibly annoying, and it can get programmers incredibly angry at each other.
3) 1/3 * 3 = 1 vs. 0.333… * 3 = ?
So this one is a less tech nerd thing and more of a math nerd thing. Essentially, when you take 1/3 and multiply it by 3, you get 1. However, as soon as you convert one third into decimal (resulting in 0.33 repeating), and then you multiply it by three, what do you wind up with? To me, it equals 1. However, some others would argue that it equals 0.999… To me, 0.999… = 1, due to the transitive property. Here is proof to describe why this is:
| Statement | Reason |
|---|---|
| 1/3 = 0.333… | Conversion to decimal |
| 1/3 * 3 = 1 | Multiplication of fractions |
| 0.333… * 3 = 0.999… | Simple multiplication |
| 0.999… = 1 | Transitive property |
So, I hope you enjoyed this article. Make sure not to cause conflicts with your nerdy friends using this article. (At least don’t tell them that Frank from Info Toast told you about this if you do).